- 1 CHAPITRE 5 : L’UNIQUE EFFET DU HASARD SUR LA STRUCTURE ALLELIQUE - Derive genetique, etranglement, consanguinite et nombre minimum d’individus a selectionner
- 2 Preambule
- 3 Pourquoi lire ce chapitre ?
- 4 La derive genetique est naturelle
- 5 Probabilite de perdre un allele d’une generation a l’autre
- 6 Probabilite de perdre un allele sur plusieurs generations
- 7 Nombre minimum d’epis a prelever
- 8 Qu’est-ce-que l’etranglement genetique, quelles sont ses consequences ?
- 9 Dualite selection et conservation
- 10 Ce qu’il faut retenir
- 11 Source
- 12 Document realise dans le cadre du projet COVALIENCE
CHAPITRE PRECEDENT : CHAPITRE 4 : LES FORCES QUI FONT EVOLUER LES STRUCTURES ALLELIQUES : Mutation, migration, dérive génétique, sélection naturelle et consciente
1 CHAPITRE 5 : L’UNIQUE EFFET DU HASARD SUR LA STRUCTURE ALLELIQUE - Derive genetique, etranglement, consanguinite et nombre minimum d’individus a selectionner
2 Preambule
Nous avons vu dans le chapitre précédent que plusieurs grandes forces influencent et modifient la structure et la diversité allélique des populations. Les mutations et les migrations sont les deux forces qui permettent l’arrivée d’une nouvelle diversité allélique dans la population. D’autres forces comme la sélection naturelle ou la sélection consciente tendent à réduire la diversité allélique dans la grande majorité des cas. Le hasard engendré par le fonctionnement de la production des gamètes et des fécondations permet le brassage génétique dans une population en recombinant, à chaque génération, les allèles qui composent le génotype des individus. Mais ce même hasard engendre aussi, inéluctablement, la disparition des allèles… C’est la dérive génétique.

3 Pourquoi lire ce chapitre ?
En sélection paysanne, les paysans sélectionneurs évoquent souvent le risque de la dégénérescence ou celui de la perte de diversité génétique… Ils tentent souvent de contrôler ce risque par la sélection d’un nombre minimum d’individus dans la population (ce nombre varie grandement en fonction des discours). Nous allons voir dans cette partie comment le hasard peut faire varier les structures allélique, discuter de la notion de perte de diversité génétique et montrer pourquoi, en effet, la sélection d’un nombre minimum d’individus est la meilleure façon de se prémunir contre ce phénomène.
4 La derive genetique est naturelle
La dérive génétique est un phénomène naturel et aléatoire qui provoque la perte de diversité allélique d’une génération à une autre. Pour une population donnée et isolée, la dérive génétique est absolument inéluctable, c’est-à-dire que sur des temps longs (voir très longs), une population va tendre irrémédiablement vers l’homozygotie s’il n’y a pas de nouvelle création de diversité allélique (mutation). Mais ce qui nous intéresse dans cet article, ce n’est pas ce qu’il se passe sur le temps long (100aine à milliers de générations), mais ce qu’il peut se passer sur des temps courts (10aine de générations).
Mais comment est-ce qu’on perd un allèle ? Ça ne tombe pas comme ça du sac ?
La perte rapide d’allèle est le résultat d’une combinaison de trois facteurs (sans compter la sélection massale) :
l’allèle est déjà rare dans la population (on appelle « rare » un allèle présent à moins de 5% dans la population)
la population se reproduit sur un petit nombre d’individus sur plusieurs générations
le hasard (celui du tirage aléatoire lors de la formation des gamètes)
5 Probabilite de perdre un allele d’une generation a l’autre
Imaginons une population quelconque de maïs dans une parcelle. L’allèle [rouge] du gène de la couleur de l’épi est rare, il est présent à 5%. En utilisant les équations d’Hardy Weinberg (et oui toujours ! c’est la base ! Voir le chapitre 3), on peut calculer les proportions d’épis rouges, orange et jaunes dans cette population. Ici on obtient 0.25 % d’épis rouge (1 épi rouge sur 400), 9.5 % d’épis orange (38 épis orange sur 400) et 90.25% d’épis jaunes (361 épis jaunes sur 400).
![Exemple de structure allélique (5% d’allèle [rouge], 95% d’allèle [jaune]) et structure phénotypique (400 épis représentés) dans le cas d’une rareté allélique.](../../../../../img/publications/chap5/pop1.jpg)
Figure 5.1: Exemple de structure allélique (5% d’allèle [rouge], 95% d’allèle [jaune]) et structure phénotypique (400 épis représentés) dans le cas d’une rareté allélique.
Imaginons maintenant que je prélève ALÉATOIREMENT (c’est-à-dire que je ne fais pas de sélection) 100 épis dans la population et que l’on considère qu’il y a environ 400 grains par épi. Je me pose la question suivante :
« Quelle est la probabilité d’avoir perdu l’allèle rare [rouge] lors de mon prélèvement aléatoire de 100 épis parmi les 400 épis qui composent la population ? »
Voici l’équation générale pour calculer la probabilité de perdre un allèle quelconque (qu’il soit rare ou non) :
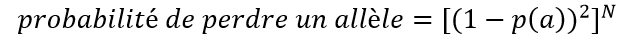
Où p(a) est la proportion de l’allèle et N le nombre de grains prélevés dans la population.
Dans le cas qui nous occupe :
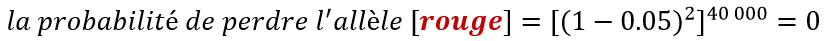
Pour les curieux voici la démonstration à partir de l’exemple présenté
Je fais donc 100 tirages aléatoires parmi les individus de la population pour obtenir la génétique maternelle. Au sein de chaque épi, il y a un tirage aléatoire pour chaque grain pour obtenir la génétique du gamète femelle. Il y a 100% de chance de tirer le gamète [rouge] si le génome maternel est RR, 50% de chance si le génome est RJ et 0% de chance sur le génome est JJ. Pour chaque épi, il y a 400 tirages (1 tirage par futur grain).
Chacun des grains sera fécondé par un pollen différent issu du nuage pollinique. Dans ce nuage il y a 5% de chance de tomber sur un pollen portant l’allèle [rouge] et 95% de chance de tomber sur un pollen portant l’allèle [jaune].
Si l’on ne s’intéresse qu’à la probabilité, on peut dire que dans cette situation, nous faisons environ 40 000 tirages de couples d’allèles. Sur 40 000 grains, en moyenne 100 grains seront de génétique RR et 3620 grains seront de génétique RJ. Pour savoir quel est le risque de perdre complètement l’allèle R, on calcule la probabilité de ne jamais tomber sur cet allèle sur la génétique maternelle des épis et qu’aucun grain n’ai été fécondé par un pollen portant l’allèle R. Dans cette situation où l’on sélectionne 100 épis, cette probabilité est égale à 0.
Imaginons désormais que je ne sélectionne qu’un unique épi (donc 400 grains venant du même pied). Et bien cette probabilité est encore de 0. Il y a plus de chance de gagner 4 fois de suite au loto que de perdre complétement cet allèle rare en ne sélectionnant qu’un seul épi ! En fait, la probabilité de perdre l’allèle rare tombe à 0 uniquement à partir de 75 grains prélevés aléatoirement (mais pas sur le même épi).
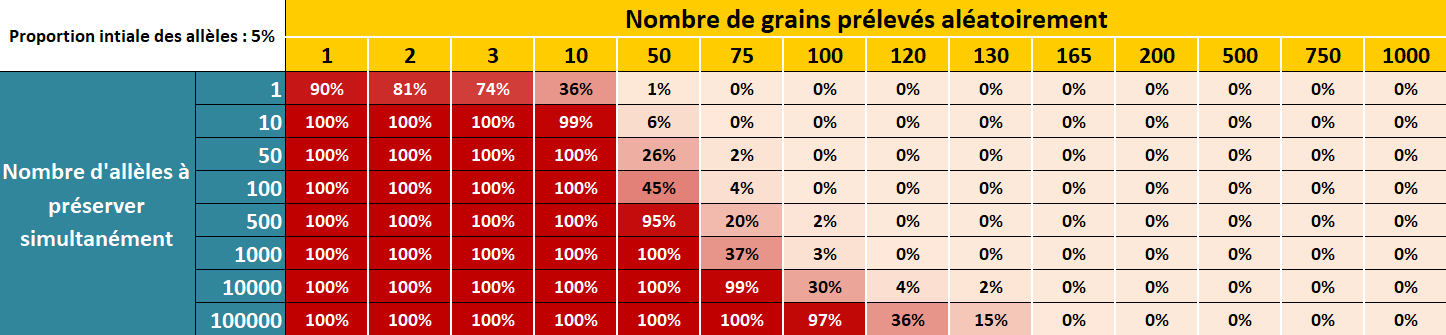
Figure 5.2: Risque de perdre des allèles rares présents initialement à 5% dans la population d’une génération à l’autre en fonction du nombre d’allèle à préserver simultanément et du nombre de grains prélevés aléatoirement dans la population.
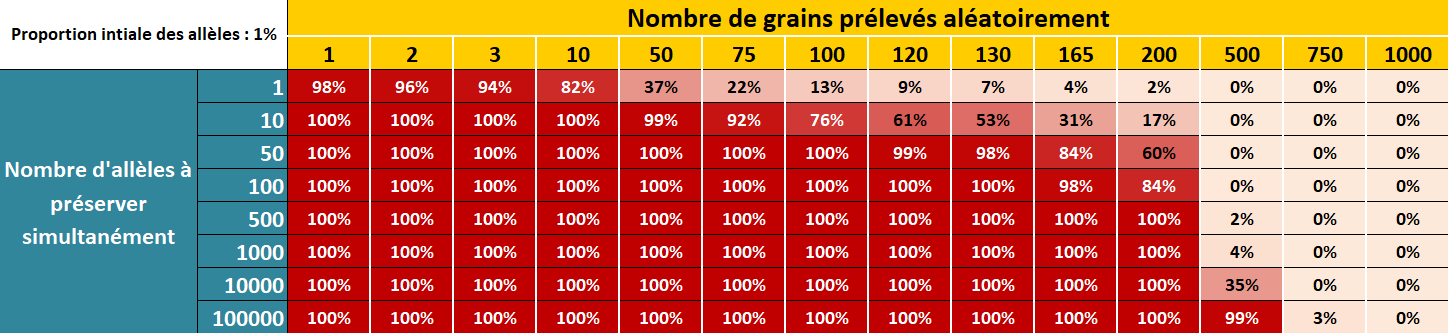
Figure 5.3: Risque de perdre des allèles rares présents initialement à 1% dans la population d’une génération à l’autre en fonction du nombre d’allèle à préserver simultanément et du nombre de grains prélevés aléatoirement dans la population.
Attention cependant, ici le calcul de probabilité est effectué sur le maïs, une espèce qui produit 400 descendants par femelle. Sur une espèce animale où les femelles donnent seulement une dizaine de descendants dans leur vie, le risque de perdre un allèle d’une génération à une autre au sein d’une population est beaucoup plus élevé ! C’est même pour cela que la sélection des races d’animaux domestiques ne peut se faire que par des programmes qui dépassent l’échelle de la ferme.
Se pencher sur la probabilité de perdre un seul allèle rare dans la population n’est pas suffisant lorsque l’on cherche à conserver la diversité génétique d’une population car il y a en réalité souvent des milliers d’allèles rares à conserver en même temps. On cherche donc le nombre minimum de grains à prélever, non pas pour préserver tel ou tel allèle rare, mais pour préserver tous les allèles rares. Les probabilités sont encore une fois assez contre-intuitives… Pour être certain à 100 % de conserver 100 000 allèles rares (il y a 55 000 gènes chez le maïs et souvent plusieurs allèles par gène) en même temps d’une génération à l’autre, il est nécessaire de prendre au minimum… 165 grains (au hasard dans toute la parcelle et pas sur un seul épi) ! Juste une poignée de grains !
L’approche probabiliste est surtout utile pour dimensionner la sauvegarde de la biodiversité cultivée ex-situ (loin des champs des paysan-nes ! Dans les conservatoires, banques de gênes, frigidaires de l’INRA, etc.). Elle prédomine encore dans de nombreuses politiques de la conservation de la biodiversité sauvage comme cultivée. Néanmoins, ces calculs et raisonnements sont insuffisants pour discuter de l’évolution des populations dans le monde paysan. Nous allons voir pourquoi dans la partie suivante [1].
6 Probabilite de perdre un allele sur plusieurs generations
On peut sentir d’intuition que l’approche par un calcul de probabilité n’est pas tout à fait suffisante pour questionner le risque de perte de diversité génétique d’une génération à l’autre. Cette intuition est bonne car ce qui nous intéresse en vérité ce n’est pas de savoir s’il y a au moins un grain possédant l’allèle rare dans notre sélection mais c’est de faire en sorte que la proportion de l’allèle rare dans la population ne bouge pas trop génération après génération.
On se pose désormais la question suivante :
« Combien d’individus dois-je prélever à chaque génération pour que la proportion de l’allèle rare [rouge] initialement présent à 5 % ne décline pas au fil des générations ? »
Pour étudier cette question nous allons utiliser une métaphore.
Imaginons un bateau à moteur naviguant sur une mer agitée. Ce navire a un cap qu’il souhaite conserver mais son gouvernail est bloqué et une fois lancé et sorti du port, il n’a plus aucun moyen pour corriger son cap.
si ce bateau est un immense paquebot, son inertie est très forte, son cap ne sera pas affecté si une petite vague frappe sa coque sur le côté. Il ne va pas dériver, ou que très légèrement.
si ce bateau est un frêle esquif, son inertie est très faible. A la moindre vague le bateau va changer de cap puis à la prochaine vague encore plus… il est balloté, il dérive. Et plus il dérive, plus la chance de dériver encore plus loin de son cap d’origine à chaque vague est forte, jusqu’au moment où il viendra s’échouer sur la plage près du port.
Pour revenir à l’évolution des populations, la taille du bateau évoque la taille de la population, le cap évoque la proportion d’un allèle quelconque dans la population et les vagues représentent une perturbation aléatoire qui correspond à la formation des gamètes et aux fécondations lors de la transmission de l’information génétique entre les générations.
6.1 Si on preleve un seul epi à chaque generation
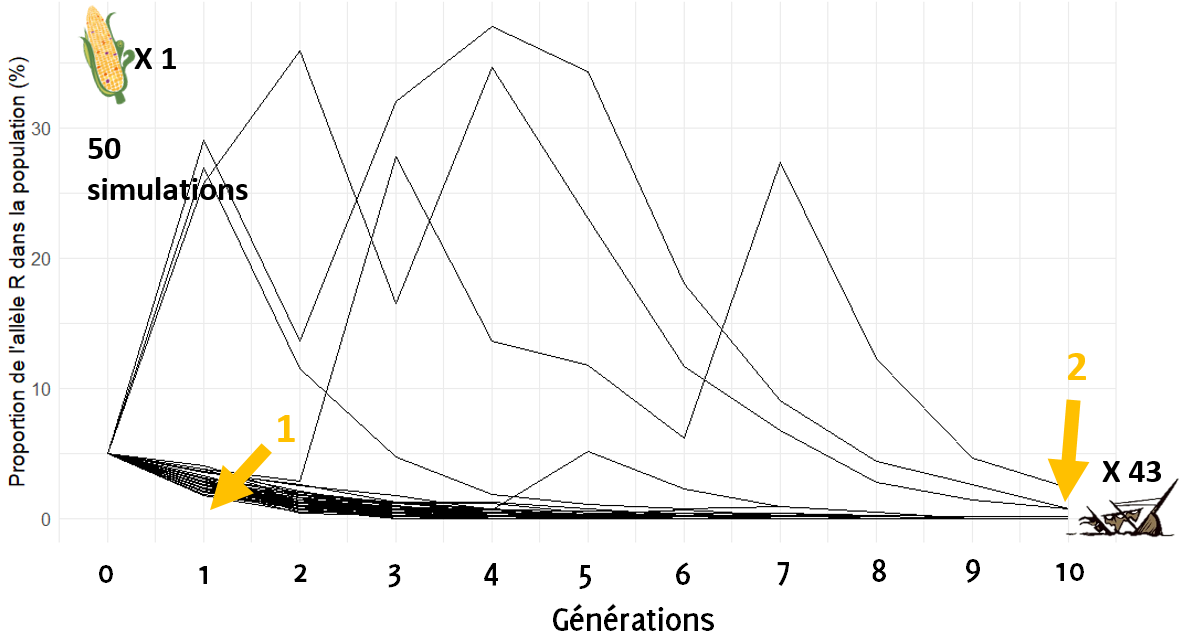
Pour chaque simulation, on part d’une population de très grande taille (+ de 10 000 plantes) avec une proportion initiale de l’allèle rare à 5 %, c’est la génération 0. Pour constituer la génération 1, on prend UN UNIQUE ÉPI au hasard dans cette population. Cet épi possède 400 grains, on ressème ces 400 grains pour constituer une nouvelle population. Pour constituer la génération 2, on prélève de nouveau 1 épi au hasard parmi les 400 plantes de la génération 1. On constitue ainsi, par répétition 10 générations. Pour chaque génération, on mesure la proportion de l’allèle rare. Ici sont simulées 50 trajectoires d’évolution de structure allélique : c’est comme si on avait envoyé 50 bateaux à la mer et qu’on regardait où chacun des bateaux arrive après un certain temps. Si le bateau arrive à 0, c’est qu’il s’est échoué : l’allèle R dans la population a été perdu.
On voit dans un premier temps (1 sur le graphique) que l’allèle rare n’est jamais perdu à la génération 1, ce qui confirme ce que nous avons vu dans la partie 2 du chapitre. Mais on voit dans un second temps (2), qu’au fil des générations, la proportion de l’allèle rare tend dans la grande majorité des cas vers 0 et le 0 est presque toujours atteint si on pousse la simulation à plus de 10 générations. Ici, dans 43 simulations sur 50, la proportion de l’allèle rare atteint 0 % : beaucoup de bateaux se sont échoués.
6.2 Si on preleve 10 épis ou 100 epis a chaque generation
Regardons ce qu’il se passe désormais si l’on augmente la taille de l’échantillon prélevé à chaque génération au nombre de 10 épis (on augmente la taille du bateau).
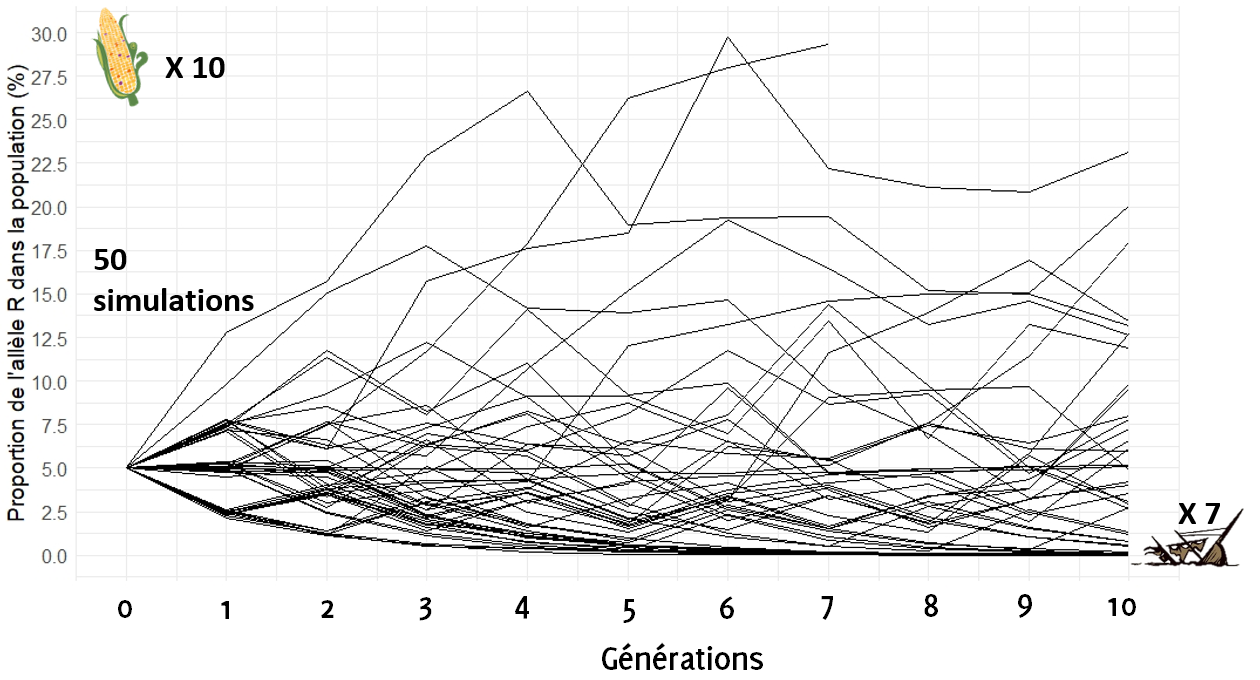
On remarque que plus on augmente la taille du prélèvement, moins les trajectoires arrivent proches de 0 % au bout de 10 générations (7 ce sont échoués) : la majorité des bateaux « restent dans la course » ! Mais est-ce suffisant ? Le risque de perdre l’allèle R semble encore assez élevé beaucoup des trajectoires tendent toujours vers 0…
Et si on augmente à 100 épis.
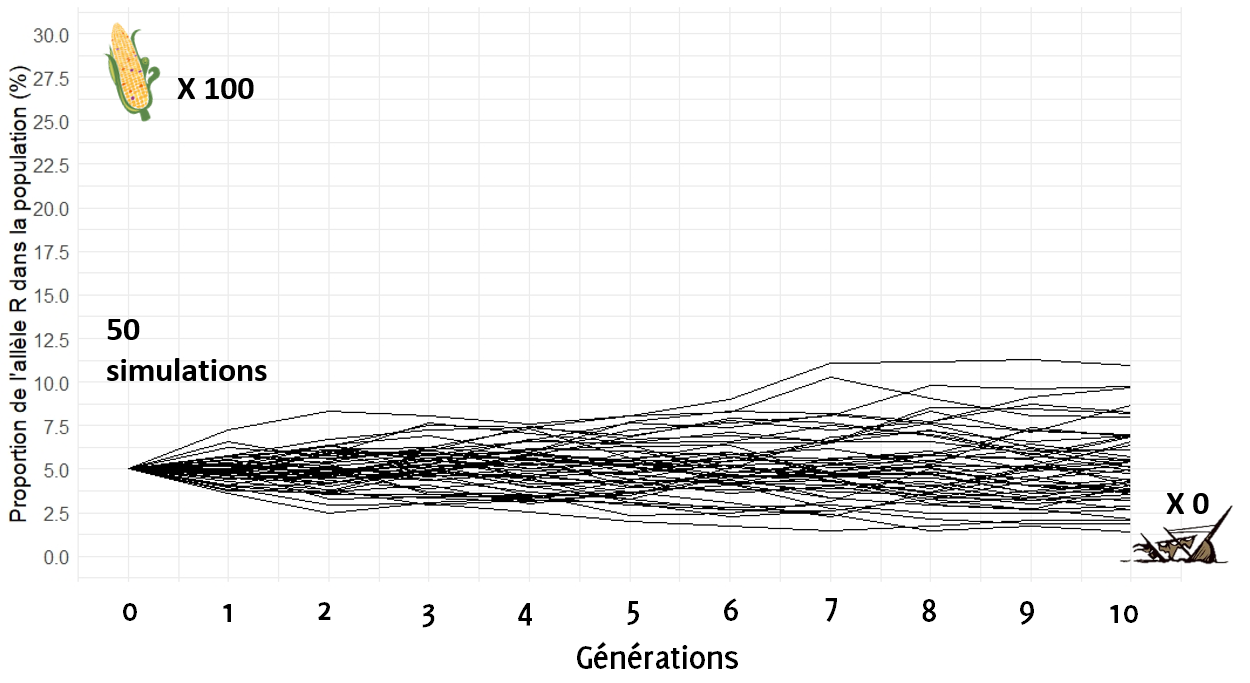
En prélevant 100 épis à chaque génération, on remarque que dans aucune des situations la proportion de l’allèle R n’atteint 0 % (aucun des paquebots ne s’est échoué) au bout de 10 générations. De plus, les trajectoires dévient peu du cap initial : au bout de 10 générations, les proportions de l’allèle R dans la population restent centrées sur 5%.
7 Nombre minimum d’epis a prelever
En sélection paysanne du maïs population, la thématique du nombre d’épi minimum à sélectionner pour constituer la génération suivante est récurrente (dans l’objectif d’éviter la dérive génétique, qui correspond au même objectif que celui de la conservation de la diversité). Il n’existe pas de réponse toute faite car la notion de risque de dérive génétique sur une population fermée est subjective. Chaque paysan devra juger le risque qu’il considère comme acceptable sachant que traduire ce risque en terme agronomique (perte de vigueur, perte de potentiel de rendement,…) est presque impossible et certainement très différent d’une population à une autre.
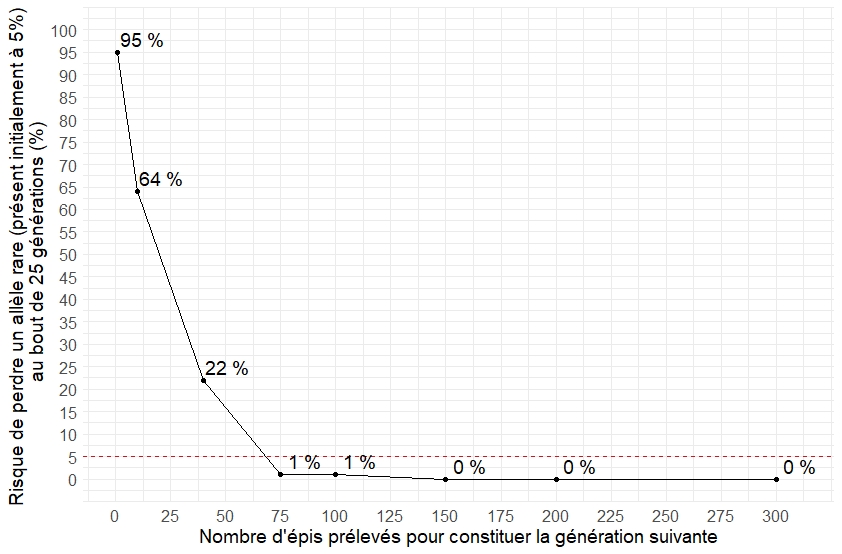
Cette figure est réalisée grâce à une grande série de simulations. Elle représente le risque de perdre un allèle rare initialement présent à 5% au bout de 25 générations en fonction du nombre d’épis qui constituent la génération suivante. On note que la diminution du risque est très rapide quand on passe d’1 épi prélevé par génération à 40 épis prélevés par génération, puis la diminution du risque est beaucoup plus anodine quand on passe de 75 épis à 150 épis. Enfin on remarque que le risque est nul à partir de 150 épis.
7.1 Conservation simultanée d’allèles rares au bout de 25 générations
Les lecteurs et lectrices affutés auront certainement remarqué que la recommandation précédente du nombre minimal d’épis à sélectionner pour constituer la génération suivante se base sur une démonstration pour conserver 1 unique allèle rare au bout de 25 générations. Mais qu’en est-il lorsque l’on souhaite conserver 1000 ou 10 000 allèles rares de façon simultanée ? Avec 100 épis, il n’est pas possible d’assurer la conservation simultanée de 1000 allèles rares dans la population. Mais avec 200 épis, le risque de perdre au moins un allèle rare parmi 1000 au bout de 25 générations se situe entre 0 et 10%.
Rappelons que ce modèle fonctionne pour une population fermée, reproduite année après année en vase clos. Notons que dans de nombreuses cultures paysannes traditionnelles, les paysans « ré-enrichissent » leurs populations en ajoutant de temps en temps un peu de semence extérieure à la population (principe de la migration vue au chapitre 4). De plus, bien que le pollen de maïs soit un pollen lourd et ne se dépose la plupart du temps qu’à quelques mètres de la plante, une très faible dose peut tout de même voyager très loin et sera capable de féconder par-ci par-là un grain de maïs d’une autre population ; de ce fait, les populations de maïs n’évoluent en réalité jamais complètement sous cloche.
Ma conclusion personnelle sur cette notion est que la dérive génétique ne semble pas être une menace tangible qui pèserait sur les populations de maïs des paysans tant qu’au moins 150 épis sont prélevés. Le risque me semble complètement nul si on prélève 300 épis : un compromis est à trouver sur chaque ferme entre le temps de travail alloué à la sélection (3 fois plus de travail à prendre 300 épis que 100 épis) et la perception du risque de dérive. Il y a un second intérêt à ne pas prendre trop peu d’épis, cette fois-ci en sélection massale, que nous développerons dans les chapitres suivants.
On note que c’est surtout l’action répétée de reproductions sur des échantillons avec peu d’individus qui provoquent la perte d’allèle mais pas la reproduction ponctuelle sur des effectifs réduits que l’on appelle parfois « étranglement génétique », une notion différente de la dérive génétique.
8 Qu’est-ce-que l’etranglement genetique, quelles sont ses consequences ?
En science des populations, on parle d’un étranglement génétique quand on observe que la proportion d’un caractère phénotypique change drastiquement d’une génération à l’autre par un phénomène qui aura supprimé la majorité d’une population (c’est-à-dire une forte mortalité dans la population avec peu de survivants). Ce phénomène est ponctuel et exceptionnel.
Notons bien que cela ne correspond pas à de la perte d’allèle ! Pour s’en convaincre, il suffit de retourner voir la figure lors de la simulation de reproduction avec 1 épi : ici on provoque en vérité un étranglement génétique à chaque génération (donc cela n’a rien de ponctuel) mais quand c’est ponctuel (entre la génération 0 et la génération 1), il n’y a pas de perte d’allèle.
Prenons un autre exemple : dans notre population, présentée en début de chapitre, composée d’un épi rouge parmi 400, imaginons que vous sélectionnez cet unique épi rouge et que vous le confiez à un.e ami.e pour qu’il se constitue une nouvelle population. Vous provoquez ici un étranglement génétique. Votre ami.e se retrouvera avec une population de maïs bien différente de la vôtre. Mais sera-t-elle uniquement constituée d’épis rouges ?
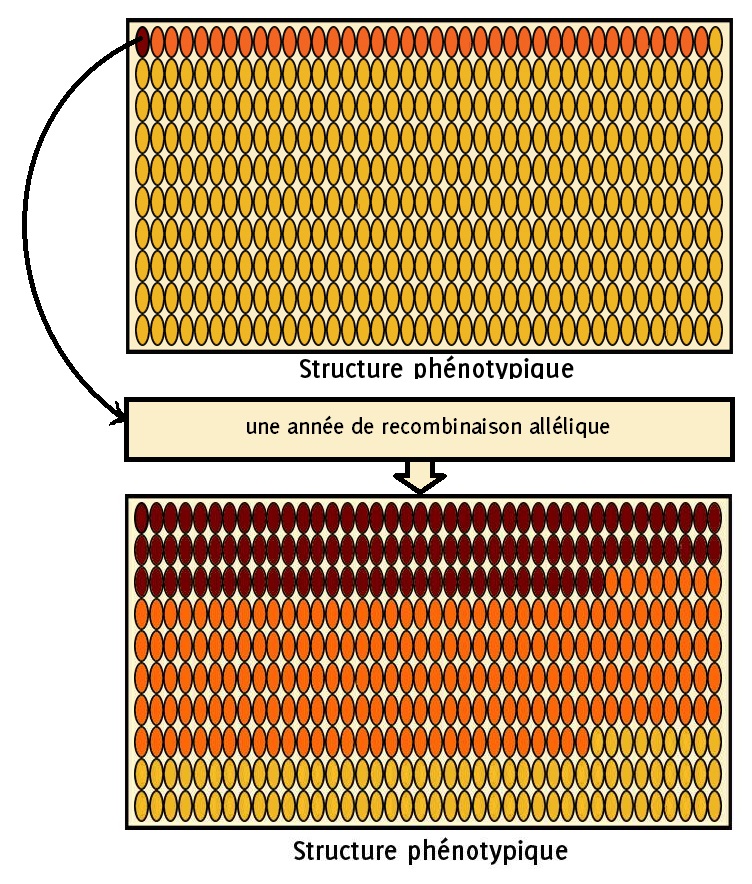
Figure 8.1: (Avertissement! Cette simulation d’étranglement est réalisée par des professionnels, n’essayez pas de le reproduire à la maison)
Pas du tout ! Au bout d’une génération, il y aura environ 28 % d’épis rouges, 49 % d’épis orange et 23 % d’épis jaunes ! On est loin d’avoir perdu l’allèle jaune !
(Et si on prend un épi jaune dans la population initiale, on obtient au bout d’une génération : 1 épi rouge pour 2000 épis, 97 épis orange pour 2000 épis et le reste d’épis jaunes).
Nous n’allons pas détailler les calculs ici qui nous permettent de calculer les proportions d’épis dans cette nouvelle population. Vous avez tous les éléments sous la main pour le faire vous-même ! Petite astuce : on a besoin de ce bon vieux Hardy et de son copain Weinberg (chapitre 3).
L’étranglement génétique est un processus réversible car il ne provoque pas la perte d’allèle (sauf cas extrême où on réduirait la population à une dizaine de grains) mais c’est un évènement qui n’est pas anodin pour autant.
Les modifications drastiques des proportions alléliques de la population produisent des modifications fortes dans les phénotypes et proportion des phénotypes dans la population (comme dans l’exemple présenté), les caractéristiques de la population changent et ne peuvent plus avoir grand-chose en commun avec la génération précédente, ce n’est, quelque part, plus la même variété… Un étranglement génétique peut alors annihiler complètement dix ans de travail de sélection qui visait justement à obtenir des équilibres et des combinaisons alléliques bien particulières.
De plus, un étranglement génétique pourra provoquer de la consanguinité, c’est-à-dire une plus grande probabilité de rencontre entre deux allèles défaillants pour un même gène. Cette consanguinité se traduira possiblement par une proportion plus élevées de pieds sans épis, de plantes chétives, d’épis mal formés, d’anomalies florales,… et donc une baisse de productivité à l’échelle du peuplement végétal. La proportion de ces « mauvais » allèles diminuera petit à petit au fil des générations sous l’effet de la sélection naturelle et de la main du sélectionneur.

9 Dualite selection et conservation
Dans cet article, nous avons présenté le mécanisme de dérive génétique sous l’unique effet du hasard et avons vu comment le contrecarrer par un nombre minimum d’individus à prélever aléatoirement. Cependant, les paysans et paysannes sélectionneurs effectuent une sélection chaque année pour adapter leur(s) variété(s) à leur(s) objectif(s) : une action qui n’est justement pas hasardeuse. Dans une situation de sélection paysanne, la dérive génétique sera donc plus forte et plus rapide sur les allèles liés à des caractères phénotypiques antinomiques avec les objectifs du sélectionneur. Par exemple, la sélection pourra être responsable de la disparition de l’allèle qui code pour la couleur jaune si le paysan ne conserve que les grains blancs, ou bien les allèles responsables de la tendreté de la tige pourront disparaître si la sélection favorise les plantes aux tiges rigides, etc. Cependant, même si le sélectionneur opère une sélection « sérieuse » sur un caractère phénotypique particulier, il lui sera tout de même bien compliqué de faire disparaître complètement un allèle responsable d’un caractère non souhaité.
Selon moi, ce risque de perte de diversité allélique, sous l’effet de la sélection, n’est pas un sujet qui doit préoccuper les paysans qui cultivent des variétés populations (du moment où une 100aine d’épis sont sélectionnés) dans la mesure où il existe une multitude de variétés et qu’une même variété est souvent cultivée par plusieurs agriculteurs. Cette préoccupation doit être portée de façon plus globale, collective et systémique en veillant à ce que les populations et les variétés reproductibles (re)trouvent leur place dans les campagnes.
Pour faire le parallèle avec la biodiversité sauvage : discuter de la dérive génétique au sein d’une population de maïs c’est comme discuter de la taille de la population à avoir dans un zoo pour préserver une espèce en danger plutôt que de discuter de la préservation des habitats naturels de cette espèce et d’assurer la connectivité entre les différentes communautés sauvages…
10 Ce qu’il faut retenir
La dérive génétique est un processus naturel et aléatoire qui entraîne la perte d’allèle sur une population fermée. Ce phénomène est directement lié à la quantité d’individus parmi la population qui constituera la génération suivante.
La conservation de la diversité allélique au sein d’une population (ou variété, ou espèce) est un enjeu majeur de la conservation de la biodiversité sauvage ou cultivée. Lutter contre la dérive génétique permet dans une moindre mesure de conserver tout le potentiel d’adaptabilité d’une variété à des contextes agro-systémiques présents et futurs et, pour les plantes allogames, d’éviter la dégénérescence vers la consanguinité d’une population.
Ainsi, cette variable du nombre d’individus est incontournable pour construire et interroger les pratiques de conservation de patrimoines génétiques. Cependant, vouloir conserver absolument telle quelle une variété est une vision passéiste de la biodiversité qui ne rend pas compte des autres forces évolutives indispensables au vivant comme la mutation (unique processus de création allélique), la migration (ajout d’allèles à une population en contact avec une seconde population) et la sélection naturelle.
En pratique :
La reproduction d’une population sur de petits effectifs entraîne rapidement une dérive génétique, c’est-à-dire une tendance à l’homozygotie ou, autrement dit encore, de la consanguinité. La meilleure façon de se prémunir de ce risque est de conserver un nombre minimum d’individus prélevés pour constituer la génération suivante. Avec 150 épis prélevés, le risque est très faible, avec 300 épis prélevés le risque est certainement nul.
L’étranglement génétique c’est la reproduction ponctuelle d’une population qui repose sur un petit nombre d’individus. Ce phénomène ne cause pas la perte d’allèles (donc de diversité), il est alors réversible mais risque de faire changer grandement les caractéristiques de la population et de provoquer de la consanguinité sur plusieurs générations.
À partir du moment où les populations ne sont pas reproduites avec des effectifs trop faibles, les paysans et paysannes sélectionneurs sont invités à ne pas trop s’inquiéter de la dérive génétique et plutôt profiter de la diversité génétique des populations pour les adapter à leur système par la sélection paysanne.
11 Source
[1] J. Crossa, « Methodologies for estimating the sample size required for genetic conservation of outbreeding crops »,
12 Document realise dans le cadre du projet COVALIENCE
NOEL Robin (2021). Chapitre 5 : L’unique effet du hasard sur la structure allélique. Dérive génétique, étranglement, consanguinité et nombre minimum d’individus à sélectionner. Projet Casdar Covalience. 9 pages.
Contact mail auteur : biodiversite@agrobioperigord.fr http://itab.asso.fr/programmes/re-covalience.php