- 1 CHAPITRE 3 : TRANSMISSIBILITE DE L’INFORMATION GENETIQUE A L’ECHELLE D’UNE POPULATION ALLOGAME Ou l’evolution de la structure allelique
- 2 Resume
- 3 Comment caracteriser genetiquement une population de mais
- 4 Les forces et les limites des equations de l’equilibre d’Hardy-Weinberg
- 5 Premier exercice de familiarisation avec les equations de Hardy-Weinberg
- 6 Second exercice pour prevoir le résultat d’une selection sur la couleur de l’epi
- 7 Ce qu’il faut retenir
- 8 Document realise dans le cadre du projet COVALIENCE
CHAPITRE PRECEDENT : CHAPITRE 2 : LA SEXUALITE DU MAIS, LA TRANSMISSION DES GENES D’UNE GENERATION A L’AUTRE ET LE BRASSAGE GENETIQUE
1 CHAPITRE 3 : TRANSMISSIBILITE DE L’INFORMATION GENETIQUE A L’ECHELLE D’UNE POPULATION ALLOGAME Ou l’evolution de la structure allelique
2 Resume
À partir des connaissances sur la transmissibilité des caractères à l’échelle des individus, cet article présente les mécanismes qui permettront de comprendre et de prévoir l’évolution des génotypes et phénotypes au sein d’une population de plantes allogames comme le maïs.
2.1 Pourquoi lire ce chapitre
Nous avons vu comment, à travers le fonctionnement de la formation des gamètes et de la fécondation, certains caractères phénotypiques étaient transmis d’une génération à l’autre et comment les différentes formes d’expression des gènes (structuration ou régulation) et des allèles (dominant, récessif, additif) influencent sur les probabilités de retrouver tel ou tel phénotype dans la descendance. Nous avons appliqué ce raisonnement sur des croisements entre deux individus dont on connaît le génome. Maintenant, nous allons voir comment raisonner à l’échelle d’une population d’individus qui se croisent aléatoirement tous entre eux.
En prenant du recul et en raisonnant à l’échelle d’une population, nous serons en mesure de :
prévoir la proportion de différents phénotypes dans la descendance en fonction de différentes opérations de sélection
comprendre pourquoi parfois un phénotype « disparu » dans notre population peut réapparaître plusieurs générations après

4 Les forces et les limites des equations de l’equilibre d’Hardy-Weinberg
Pour que les équations de Hardy-Weinberg fonctionnent, il faut cependant respecter des hypothèses de départ.
la population est de taille infinie (ou autrement dit de très grande taille) ;
la rencontre des gamètes et la formation des « couples » est complètement aléatoire et les individus sont répartis de manière homogène au sein de la population. On parle dans cette situation de panmixie ;
il n’y a pas de migration de gamètes qui viennent de l’extérieur ;
il n’y a pas de mutation sur les allèles considérés ;
il n’y a pas de chevauchement des générations (il n’y a pas d’accouplement entre les différentes générations) ;
il n’y a pas de sélection des individus (et oui, car sinon on déstructure complètement les proportions).
L’équilibre d’Hardy-Weinberg est ce qu’on appelle « un modèle », c’est-à-dire que c’est une simplification de la réalité pour pouvoir faire des prédictions et estimations. Par « simplification de la réalité », on entend donc que les équations sont partiellement, voire totalement, fausses en fonction du degré de respect des hypothèses de départ. Par exemple, chez le maïs, on sait qu’il y a une part non négligeable d’autofécondation (le pollen produit par un pied féconde les soies du même pied) : on ne respecte pas l’hypothèse de la panmixie et les équations ne fonctionnent donc pas parfaitement. On peut parfaitement agrémenter le modèle pour intégrer cette nouvelle donnée mais on apporte ainsi de la complexité. Un modèle résulte toujours d’un équilibre subjectif entre simplicité, robustesse et précision de la prédiction.
5 Premier exercice de familiarisation avec les equations de Hardy-Weinberg
5.1 Enonce
Les individus de génétique [jaune-jaune] ont un épi jaune, les individus de génétique [jaune-rouge] ont un épi orange et les individus de génétique [rouge-rouge] ont un épi rouge. L’expression des allèles entre eux est de type additif (c’est-à-dire que le phénotype d’un individu de génotype [rouge-jaune] sera le résultat de l’expression de la sommes des allèles : jaune + rouge = orange. Voir chapitre 2).
Vous faites un échantillonnage de votre population de maïs en prélevant au hasard 200 épis. Parmi ces 200 épis, vous comptez 25 épis rouges.
Calculez la proportion d’allèles jaune et rouge dans la population. Sans avoir à les compter, calculez la proportion d’épis jaunes et d’épis orange dans la population.
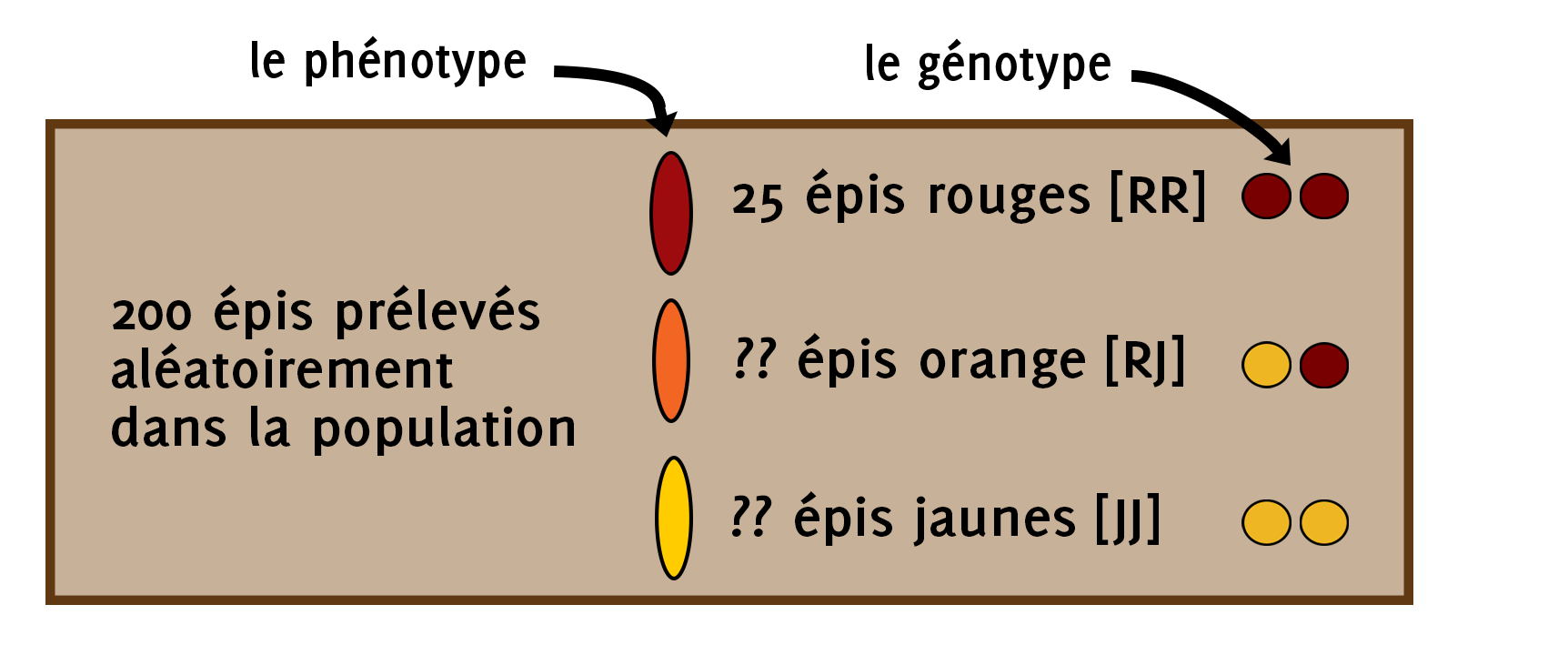
5.2 Reponse
● On sait que si l’épi est rouge, c’est que son génotype est [rouge-rouge]. On commence par calculer la proportion d’individus rouge-rouge dans la population à partir de notre échantillon.
P(RR) = 25 / 200 = 0,125 = 12,5%
● On va ensuite calculer la proportion d’allèles [rouge] et [jaune] dans la population.
On sait que p(RR) = p(R) x p(R) que l’on peut aussi écrire : p(RR) = p(R)^2 Pour connaître p(R), on « inverse » l’équation. L’inverse du « carré »(^2) c’est la « racine carré » (^(1/2)).
Ainsi : p(R)= (p(RR))^(1/2)= 0,125^(1/2)=0,35
La proportion d’allèles rouges dans la population est de 35%
Et p(J) = 1 – p(R) = 1 – 0.35 = 0.65
La proportion d’allèles jaunes dans la population est de 65%
● Maintenant que nous avons la proportion des allèles [rouge] et [jaune] dans la population, on peut calculer la proportion des génotypes JJ et RJ
P(JJ) = p(J) x p(J) = 0.65 x 0.65 = 0,42 = 42%
Il y a 42% d’épis jaunes dans la population.
● On a désormais deux possibilités pour calculer la proportion des individus à la génétique RJ (donc épis orange) dans la population.
Soit on prend la formule p(JJ) + p(RR) + p(JR) = 1 Où p(JR) = 1- p(JJ) – p(RR) = 1 - 0.42 – 0.125 = 0.455 = 45,5%
Soit on prend la formule p(JR) = p(J) x p(R) x 2 p(JR) = 0.65 x 0.35 x 2 = 0.455 = 45,5%
Dans cette population, en sachant qu’il y a 25 épis rouges sur 200 épis prélevés aléatoirement, nous avons pu déduire avec les équations de Hardy Weinberg que : la proportion d’allèles rouges est de 35%, la proportion d’allèles jaunes est de 65%. La proportion d’épis rouges est de 12,5%, la proportion d’épis orange est de 45,5% et la proportion d’épis jaunes est de 42%.
6 Second exercice pour prevoir le résultat d’une selection sur la couleur de l’epi
6.1 Enonce
Nous reprenons les postulats de l’exercice précédent :
Les individus de génétique JJ ont un épi jaune.
Les individus de génétique RJ ont un épi orange.
Les individus de génétique RR ont un épi rouge.
La proportion d’allèles rouges dans la population est de 35% et la proportion d’allèles jaunes est de 65%
Question 1 : si je ne sélectionne dans cette population que les épis rouges, quelle seront les proportions d’épis jaunes, orange et rouges dans la descendance ?
Question 2 : si je ne fais pas de sélection dans cette descendance, quelles seront les proportions d’épis jaunes, orange et rouges dans la génération suivante ?
Attention, nous rappelons que dans cet exercice la couleur de l’épi dépend uniquement de la génétique du pied qui le porte mais pas de la génétique des pollens qui fécondent chacun des grains.
6.2 Reponse
6.2.1 Question 1 :
Comme on sélectionne uniquement les épis rouges, on est sûr que les gamètes maternels produits par les plantes qui portent les épis rouges contiennent l’allèle [rouge].
Par contre, on ne sait rien de la composition génétique des pollens qui sont venus féconder la fleur femelle des plantes qui portent les épis rouges. Ces pollens peuvent venir de plantes qui portent un épi rouge, orange ou jaune.
Tout ce que nous connaissons, c’est la proportion d’allèles [rouge] et d’allèles [jaune] dans la population. Comme toutes les plantes produisent des pollens dans des quantités que nous considérons identiques, alors la proportion de grains de pollen portant un gamète rouge est égale à la proportion de gamètes rouges dans la population. Il en est de même pour le gamète jaune.
Il y a donc 35% de chance pour que les soies soient fécondées par un pollen portant l’allèle [rouge] et 65% de chance pour que les soies soient fécondées par un pollen portant l’allèle [jaune].
On peut ainsi faire le tableau de fécondation et prédire les différentes proportions des phénotypes et génotypes dans la génération suivante.
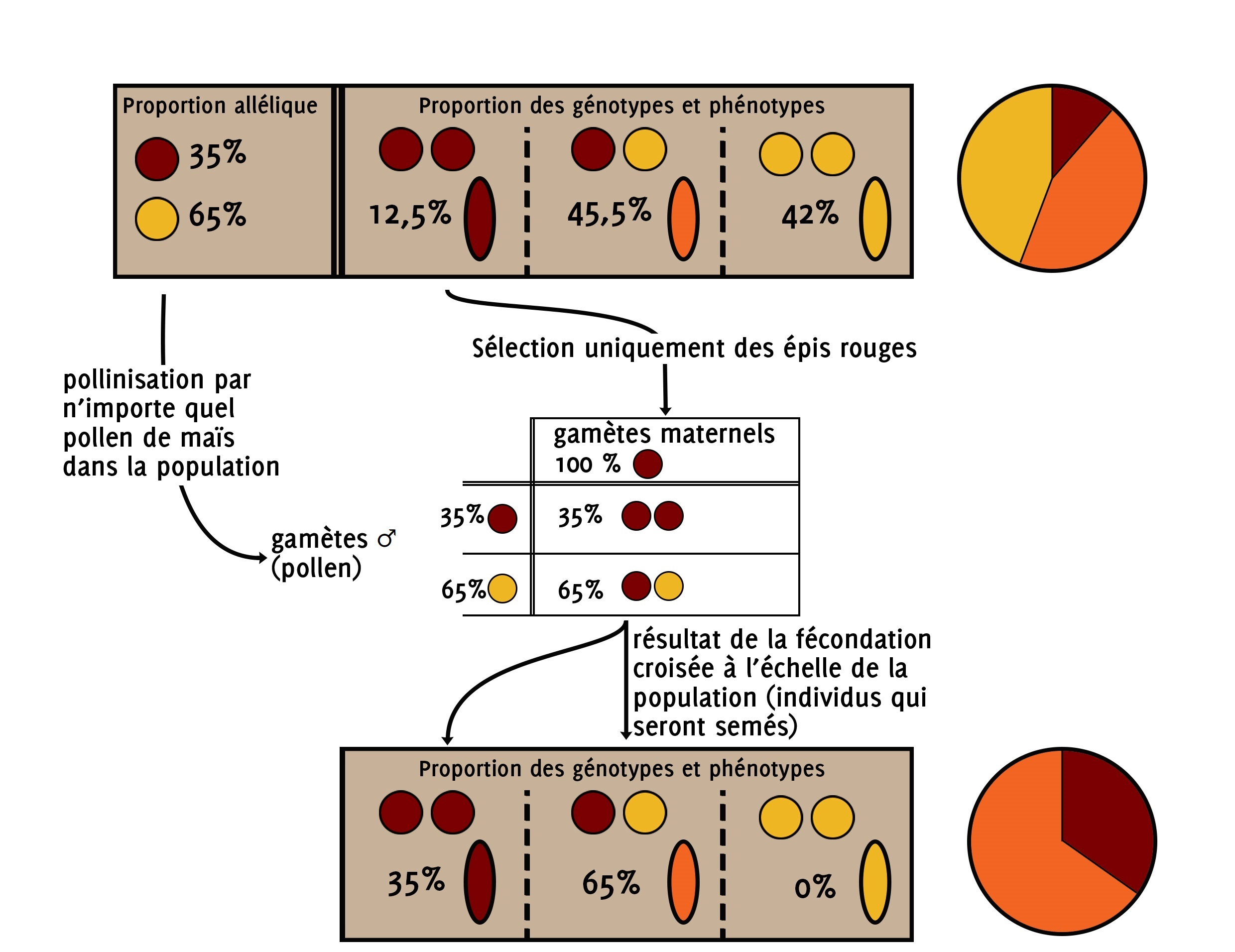
6.2.2 Question 2 :
Dans une population allogame, tous les individus se recroisent aléatoirement chaque année. C’est comme si l’on remélangeait toutes les billes dans le sac pour faire le nouveau tirage qui constituera la génération suivante. Notre nouvelle population de départ est ici constituée de 35% d’individus à la génétique (RR) et 65% d’individus à la génétique (RJ).
Pour connaître le résultat du brassage, il nous faut connaître les proportions d’allèles rouges et jaunes dans la population. Mais nous ne pouvons pas utiliser ici les équations de l’équilibre d’Hardy Weinberg pour calculer ces proportions car il y a eu une sélection (cela fait partie des hypothèses de départ du modèle). Il faut donc ruser !
On sait d’office qu’il y a au moins 35% d’allèles rouges dans la population car nous avons 35% d’individus qui ne possèdent que des allèles rouges. Les 65% des individus restant possèdent un allèle rouge et un allèle jaune. C’est moitié moitié.
Ainsi, la proportion d’allèles rouges dans la population est égale à 35% plus la moitié de 65%. P(R) = 0.35 + 0.5 x 0.65 = 0,675 = 67.5%
Et la proportion d’allèles jaunes est égale à la moitié de 65%. P(J) = 0.5 x 0.65 = 0.325 = 32.5%
On peut de nouveau utiliser les équations de l’équilibre de Hardy Weinberg car en passant par le calcul des proportions alléliques, c’est comme si « on remettait tout à plat ».
P(RR) = p(R) x p(R) = 0.675 x 0.675 = 0.455 = 45.5 %
P(JJ) = p(J) x p(J) = 0.325 x 0.325 = 0.106 = 10.5 %
P(RJ) = p(R) x p(J) x 2 = 0.325 x 0.675 x 2 = 0,44 = 44 %
Dans la génération qui suivra le brassage aléatoire du résultat de votre première sélection sur les épis rouges, vous retrouverez 45,6 % d’épis rouges, 44 % d’épis orange et 10,5 % d’épis jaune.
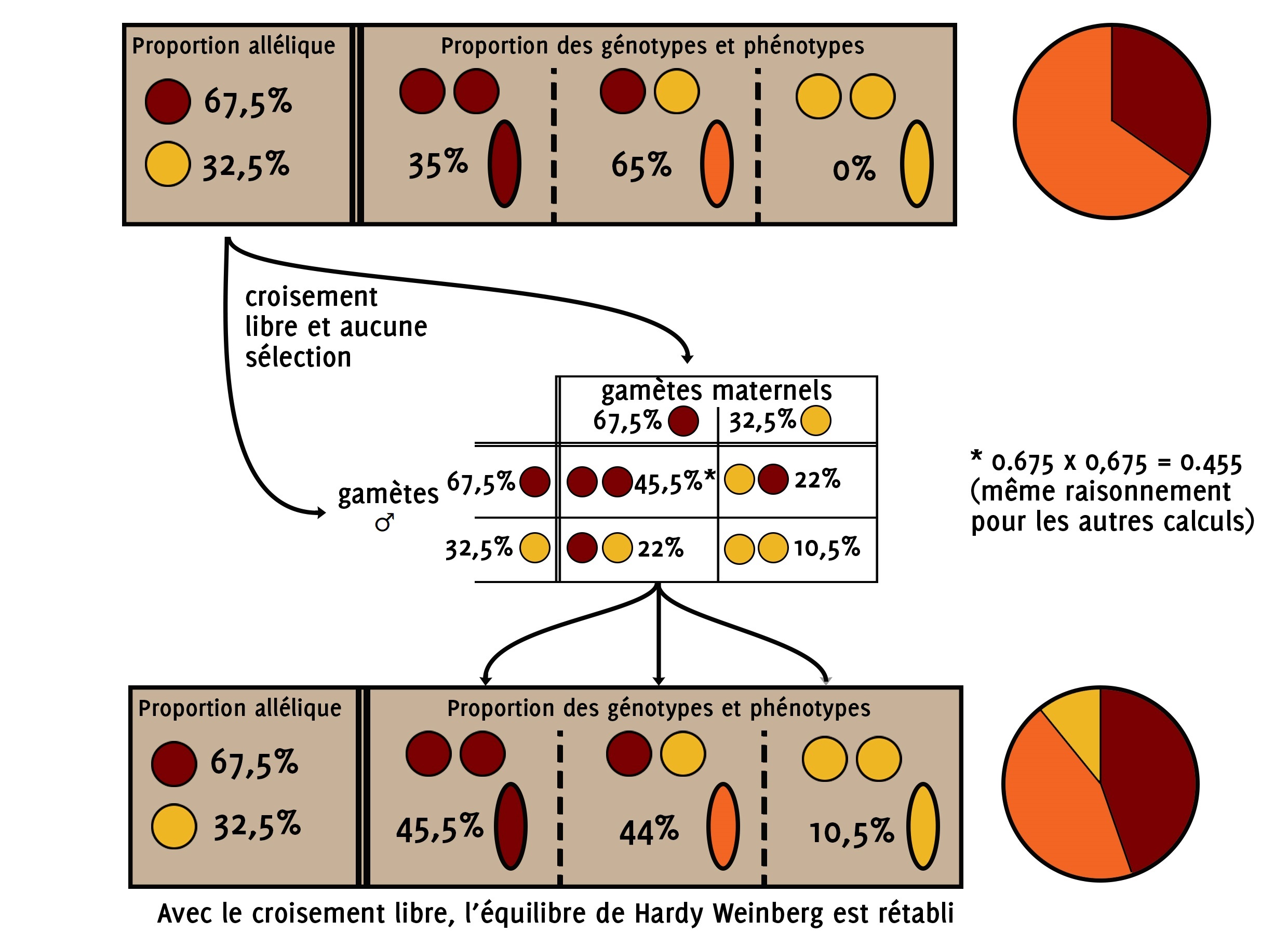
7 Ce qu’il faut retenir
Quand on étudie la génétique à l’échelle d’une population, on parle surtout en termes de probabilités et de proportions.
La proportion des génotypes et des phénotypes dans la population dépend de la proportion des allèles dans la population.
Les équations d’Hardy-Weinberg permettent d’établir le lien entre ces différentes proportions.
Les équations d’Hardy-Weinberg constituent un modèle simple et, même si la réalité est toujours plus complexe, sa qualité prédictive est élevée.
Grâce aux équations, on peut prédire le résultat de différentes sélections et recombinaisons aléatoires sur les proportions de différents phénotypes dans la population.
En fonction des situations, on peut voir comment un phénotype peut disparaître temporairement dans une population et réapparaître la génération suivante grâce aux recombinaisons alléliques.
CHAPITRE SUIVANT : CHAPITRE 4 : LES FORCES QUI FONT EVOLUER LES STRUCTURES ALLELIQUES - Mutation, migration, dérive génétique, sélection naturelle et consciente
8 Document realise dans le cadre du projet COVALIENCE
NOEL Robin (2021). Chapitre 3 : Transmissibilité de l’information génétique à l’échelle d’une population allogame. Projet Casdar Covalience. 9 pages
Contact mail auteur : biodiversite@agrobioperigord.fr

3 Comment caracteriser genetiquement une population de mais
Comme nous l’avons vu au chapitre 1, pour chaque gène, il en existe différentes versions : les allèles. Dans une population, il peut y avoir un grand nombre de versions par gène mais chez le maïs, qui est une plante diploïde (voir chapitre 2), chaque individu ne porte pour un gène donné que deux allèles (les mêmes ou différents).
Reprenons ici notre exemple du gène de la « couleur de l’épi ». Il existe deux allèles différents dans la population : [jaune] et [rouge] et on compte trois niveaux de combinaison allélique pour ce gène, c’est-à-dire trois génotypes. Un individu peut être de génotype [jaune-jaune], [jaune-rouge] (= [rouge-jaune]) ou [rouge-rouge] que l’on va noter plus simplement JJ, RJ et RR.
Imaginons que nous connaissons le génotype de chaque individu de la population ; nous pouvons alors compter le nombre d’allèles [rouge] et d’allèles [jaune] dans la population. On note p(R) la proportion d’allèles [rouge] dans la population. Ainsi p(R) prend une valeur comprise entre 0 (il n’y a pas d’allèle rouge dans la population donc aucun individu ne porte cet allèle dans son génome) et 1 (il n’y a que des allèles rouges dans la population donc tous les individus possèdent un génotype RR).
De même, on note p(J) la proportion d’allèles [jaune] dans la population, p(J) prend aussi une valeur comprise entre 0 et 1.
Pour caractériser une population de plusieurs milliers d’individus, on peut s’intéresser, pour un gène donné, à la proportion des différents allèles présents, on parle de structure allélique de la population.
Quand il n’y a pas de pression de sélection et que la population considérée est très grande, la structure allélique de la population reste exactement la même d’une génération à une autre. La structure allélique de la descendance est la même que la structure allélique des parents. Il est donc possible de faire des liens logiques entre structure allélique et proportion des génotypes (et donc phénotypes) aussi bien sur une même génération mais aussi entre les générations.
Nous proposons la métaphore du sac de billes afin d’illustrer la notion de structure allélique. Le sac représente la population, les billes représentent les allèles (elles sont de différentes couleurs car il en existe différentes versions), les petits rectangles représentent le génotype des individus.
Il existe une série d’équations très simples qui permettent d’établir le lien entre la proportion des allèles [Rouge] et [Jaune] dans la population : la structure allélique et les proportions des génotypes JJ, RJ et RR.
Les valeurs de p(R) et de p(J) sont toujours liées l’une à l’autre : leur somme fait toujours 1. p(R) + p(J) = 1 on peut aussi écrire p(J) = 1-p(R) et réciproquement p(R) = 1-p(J)
Par exemple: il existe uniquement deux versions de gènes pour la couleur de l’épi : jaune et rouge. Si on sait qu’il y a 2% d’allèles [rouge] dans la population (p(R) = 0,02) alors on peut déduire qu’il y a 98% d’allèles [jaune] dans la population (p(J) = 1-p(R) soit p(J) = 1 - 0.02 = 0.98).
Comme la proportion allélique reste inchangée d’une génération à une autre, si on connaît la proportion des allèles jaunes et rouges dans la population : on peut prédire la proportion des individus avec une génétique jaune-jaune, jaune-rouge et rouge-rouge.
C’est encore une question de probabilité et de tirage aléatoire et nous allons utiliser la métaphore du sac à billes.
Quelle est la probabilité d’avoir un individu à la génétique jaune-jaune ? Et bien c’est la probabilité p(J) de tirer une première fois une bille jaune dans le sac multipliée par la probabilité p(J) de tirer une deuxième fois une bille jaune dans le sac.
Soit la proportion d’individus jaune-jaune dans la population est égale p(J) x p(J) ou p(J) au carré. On note alors : p(JJ) = p(J)2 où p(JJ) est la proportion d’individus à la génétique jaune-jaune). De même p(RR) (la proportion d’individus à la génétique rouge-rouge) : p(RR) = p(R)2
Il y a une subtilité sur la proportion des individus hétérozygotes p(JR) dans la population. Car c’est la probabilité de tirer la première fois une bille rouge p(R) multipliée par la probabilité de tirer la seconde fois une bille jaune p(J) mais aussi la probabilité de tirer la première fois une bille jaune p(J) multipliée par la probabilité de tirer la seconde fois une bille rouge p(R).
Ainsi p(JR) = p(J) x p(R) + p(R) x p(J) = 2 x p(J) x p(R)
Et de façon toute logique :
p(JJ) + p(RR) + p(JR) = 1
Figure 3.1: Illustration des liens entre la structure allélique de la population et la proportion des génotypes dans la population (pour une même génération ou entre les générations).
Les équations que nous venons de voir et qui établissent le lien entre structure des allèles d’une population et proportion des génotypes s’appellent les formules de l’équilibre d’Hardy-Weinberg. Ces équations sont assez incontournables en science des populations et en sélection variétale.